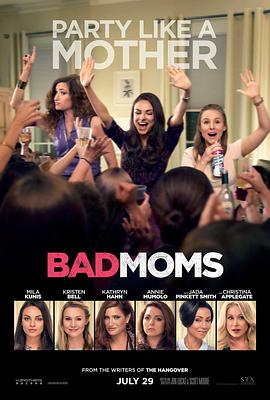费

　　阿基姆（艾迪·墨菲 Eddie Murphy 饰）是扎门达国的王子，他和侍从桑米（阿瑟尼奥·豪尔 Arsenio Hall 饰）来到美国，要在这里进行为期40天的微服访问。对于阿基姆来说，此行还有另外一个目的，他对父亲甲斐（詹姆斯·厄尔·琼斯 James Earl Jones 饰）为自己安排的婚事很是不满，所以阿基姆魔唇劫国语决定，一定要在美国找到自己的真命天女。　　幸运的是，这样的女人很快就出现了，她的名字叫做莎莉（沙里·海德利 Shari Headley 饰）。为了接近莎莉，阿基姆进入了莎莉父亲开的面包店成为了一名打工仔。莎莉有一个个性十分粗暴的男友，相比之下，她更加喜欢温文尔雅的阿基姆，正当两人的关系逐渐步入正轨之时，甲斐竟然亲临美国，阿基姆苦心恐男改造计划小说隐瞒的身份眼看就要被揭破。

妻子的死给电视台王牌主播霍华德（彼得·芬奇 Peter Finch 饰）带来Free Gay GV TV了沉重的打击，使他陷入痛苦和悲伤中无法自拔。电视台决定解雇已大武当下载经无心工作的霍华德，霍华德的老朋友麦克斯（威廉·霍尔登 Will...

该剧讲述了在经济萧条的大小西友梨背景下，一个工人阶级的家庭，一个经常被发现睡在客厅地板上的酒鬼一家之主，一个不称职的老妈，他们的女儿，18岁的菲奥纳承担下了抚养他5个弟弟妹妹责任，这对她来讲似乎是个不可能完成的任务·热闹非凡的家太原师范学院聊天记录庭日常生活夹杂着爱情，冒险，欺诈 ,温情等等有血有泪的故事。

　　这是一部以营造气氛见长的经典恐怖片，讲述1630年一个女巫和她情人被她自己的兄弟杀死。两百年后，两人复活，向她兄弟的后代（其中有一个酷似女巫）复仇。　　跟多数意大利恐怖片一样，本片的故事并不特别，但哥特式的场景阴森难忘。故事灵感来自果戈里小说。女主角一人分饰两角，暗示善恶之间只有一线之隔，演绎起来的样子就像是神情恍惚的肯尼迪夫人。　　* * * * *　　众多恐怖电影迷们都以为他们的钟爱己在Universal、Hammer、Roger Corman和其他一些著名的恐怖电影制片室和生产商摄制的各类影片中得到了实现。其实只有当你到阳光灿烂的意大利对满布阴霾的意国电影走走看看时，你才算真正经历了经典的恐怖电影。　　Black Sunday (1960) 又名 The Mask of Satan：意大利电影制作者再次着手恐怖电影的拍摄已经是四年以后了，在Re兔六电影nato Polselli同样受欢迎的《The Vampire and the Ballerina》(1960)之后，摄影师Mario Bava首次作为导演浮出水面，创作了一部代表性的恐怖电影，这宣告恐怖电影作为一种电影类型从此诞生。　　The Mask of Satan是真正小镇姑娘无删减播放意义上的恐怖电影代表作，故事大致源于果戈里的《the Viy》，它讲述一个处死二百年后的巫婆复活人世开始报复当初处死她的人们的后代，然而这个故事相对于Bava那几乎要跳出屏幕般的特殊视觉效果而言稍显次要，他的构图如此复杂，以至于影片的每一帧都可以被放大并挂在墙上，光与影的强烈对比营造出有什于Universal公司早期作品的恐怖效果，Bava创造出一出惊心动魄的神怪故事，充斥了巫婆、幽灵、秘密通道、凄叫的野狗、恶毒的公车司机甚至包括对着路人张牙舞爪的树枝。每一位看完此片的恐怖电影迷都着实大开眼界。　　这部影片在意大利取得成功并预示着Bava执导生涯的开始，它在美国经过删改后冠以《黑色星期天》（Black Sunday），同样大受欢迎。虽说它经过了修改，但基本上还是保证了原作的汁味，并一着被能在首映时有幸一睹的美国电影迷们津津乐道难以忘怀。影片取得成功的一大功劳归于片中的影星Barbara Steele，这部作品标志着Barbara Steele演艺生涯的发韧，之后她又在九部义大利恐怖电影中担纲主演，每一部都因她的表现而亮色。她那阴暗的造型、冷淡的情欲使她自然而然地适演恐怖片，由她演出的多数电影取得成功都与她的表现密不可分，她的另外几部意大利恐怖电影为：《The Horrible Dr. Hichcock》（ 1962）、《The Ghost》（1963）、《Long Hair of Death》（1964）、《 Castle of Blood》（1964）、《Nightmare Castle》（1965）和《She-Beast》 （1965）、 《Terror Creatures from the Grave》（1966）、《An Angel for Satan》武巅峰练（1966）。

　　长久以来，剧作家大卫（约翰·库萨克 John Cusack 饰）都过着郁郁不得志的生活，艺术家特有的清高让他对如今腐败混乱的话剧界充满了失望之情。为了讨好情妇奥利芙（詹妮弗·提莉 Jennifer Tilly 饰），黑帮大佬看中权利的游戏第五季了名不见经传的大卫的剧本想要投资，作为前提条件 ，大卫必须让奥利芙饰演主角。虽然奥利芙唠叨的个性和蹩脚的演技让大卫深感抓狂，但在利益面前，他痛苦的屈服了。就这样，一个奇怪的剧组诞生了。　　剧本的漏洞，女演员们之间的矛盾，男主演日益肥胖的身材都让大卫感到绝望，但令他惊奇的是，一直监视着奥利芙的保镖契奇（查兹·帕尔明特瑞 Chazz Palminteri 饰）在无意中展现了过人的编剧才能。在契奇的帮助下，被改写的剧本居然获得了盛大的成功，与此同时，契奇对由自己操刀的剧本展现出的病态执着和剧组里混乱的男女关系让大卫陷入了另一个困境……

　　女孩克里斯汀（西尔莎·罗南 Saoirse Ronan 饰）跟随着家人来到了位于加州的一间教会学校开始了她的高中生涯，虽然心中有百般的不愿意，但克里斯汀尚且没有足够的力量来反抗家人和生活的安排。在学校里，克里斯汀最好的朋友是朱丽（比妮·费尔德斯坦 Beanie Feldstein 饰），三观相近的两人无话不谈。　　克里斯汀参加了舞台剧比赛，并因此结识了名为丹尼（卢卡斯·赫奇斯 Lucas Hedges 饰）的男孩，相互吸引的两人很成都聊天室快就走到了一起。然而，这段感情最终以分手告终。为了和校园交际花珍娜（奥德娅·拉什 Odeya Rush 饰）套近乎，克里斯汀不惜撒谎，遗憾的是，谎言并不能换来真正的友谊。当克里斯汀身陷同凯尔（提莫西·查拉梅 Timothée Chalamet 饰）的感情纠葛之中时，她的家庭也在经历着艰难时期。

　　故事讲述美男男罪游记国钻石商卢卡斯(基努饰)去西伯利亚做生意时，与咖啡馆店主卡佳(安娜·2012手机免费观看乌拉鲁饰)坠入情网，然而事态却步入危险。

　　斯奈利和达利从小就是性情迥异的死对头，快播黄网址即使是长大后达利变成威风的骑警，斯奈利仍为无恶不赦的大坏蛋，在一次天堂资源最新版抢劫活动，斯奈利占据了小镇，一切都在乱无法纪的状况下进行，达利要如何解决这混乱的场面让小镇恢复平静？

　　J暖暖请多指教电视剧免费观看udge William "Billy" Priest lives in a very patriotic (Confederate) southern town. Priest plays a laid-back, widowed judge who helps uphold the law in his toughest court case yet. In the meantime, he plays matchmaker for his young nephew.

　　该作品改编自2000年同名纪录片，讲述塔米·菲（杰西卡·查斯坦 饰）和吉姆·贝克（安德鲁·加菲尔德 饰）这对夫妇作为电视福音布道家的大起大落。在上世纪70-80年代，塔米·菲和吉姆·贝克从贫寒中国内2018自拍视频在线奋起，创建了当时世界上最庞大的宗教广播电视网和一个主题公园，他们传递的爱、接纳和繁荣的主题受到人们的尊敬。塔米 · 菲以她夸张的睫毛，独特的歌声、以及她热情拥抱各行各业的人们而成为传奇。不过好景不长，经济上的不当行为、诡计多端的竞争徐文明的新浪博客对手以及性丑闻的爆发使得这对夫妇的婚姻破裂，导致他们精心构建起来的帝国开始崩塌。

<电影爱人在线观看;p>20世纪之初，高尔夫球还只是英国贵族和绅士们的游戏，底层人民没有资格染指其中，它无疑是身份和权力的象欧洲性旅行高清征。少年弗朗西斯·奥密特（Matthew Knight 饰）出身洪晓芸 张萱平民家庭，读书之余他经常担任球童贴补...

　　城扫黑风暴观看市在恢复平静后，大反派重新召集旧部卷土重来，并勾结外星恶势力朗格试图称霸地球，忍者神龟莱昂纳多（皮特·普劳泽克 Pete Ploszek 饰）、拉斐尔（阿兰·里奇森 Alan Ritchson 饰）、多纳泰罗（杰瑞米·霍华德 Jeremy Howard 饰）和米开朗基罗（诺尔·费舍 Noel Fisher 饰）与女记者艾蓓丽尔·奥尼尔（梅根·福克斯 Megan Fox 饰）、韦恩·芬威克（威尔·阿奈特 Will Arnett 饰），及面具义警凯西·琼斯（斯蒂芬·阿梅尔 Stephen Amell 饰）并肩作战打击恶徒。在史莱最新泰剧德（布莱恩·泰 Brian Tee 饰）逃脱拘留后，他与疯狂的科学家巴克斯特斯·托克曼（泰勒·派瑞 Tyler Perry 饰）及其两个笨拙的左膀右臂猪面和牛头联合，发布了一个控制世界的恶魔计划。在神龟们与史莱德及其同伙对抗的同时，他们发现自己正面临着一个更邪恶的力量大反派格朗，神龟们面对的将是宇宙级的强大对手。

　　龙卷风的暴戾和神秘吸引了大批科学家的深入研究，深入风暴中间是最危险的行为，但亦是探索龙卷风最有效的方法。乔（海伦·亨特 Helen Hunt饰）和离婚的丈夫比尔（比尔·帕克斯顿 Bill Paxton饰）就是这类“与龙共舞”的科学家，即使他们感情已经破裂，比尔也已找到新的恋人，但出于对龙卷风研究的痴迷，他们还是决定共同追逐一场俄克拉何马州的飓风，并把新研制成功的探测仪“多萝西”放到龙卷风中心收集数据第一主板o1bz手机版。　　他们驾驶着破旧的奥莉薇官网货车，带领着追风队，向最危险的地方进发。同时，另一队装备精良的人马也朝着这个方向驶去，由裘纳（加利·艾尔维斯 Cary Elwes饰）领队，在追风行动中和乔激励较劲。　　一边是志同道合的乔，一边是畏惧惊险生活的新女友，比尔在追风过程中如何重新抉择自己的感情道路？更重要的是，面对实力雄厚的对手，和随时葬身其中的龙卷风，乔和比尔如何实现自己的追风梦想？

　　文森（伊马诺尔·佩尔塞 Ymanol Perset 饰）表面看来只是一介平凡青年，却拥有着一忘忧草在线观看网身了得的射击本领，年仅二十五岁的他作为官方认可的枪械教官，深受业内同行的尊重和赞赏，前途可谓一片光明。　　某日，一位名叫米罗（乔伊·斯塔尔 Joey Starr 饰）的警察出现在了文森的身边，殊不知他的所作所为将会彻底改变这位青年的命运。接二连三的意外让文森被迫处于争斗的漩涡中心，不断沉浮于阴谋和罪恶之中。特警队指挥官查韦斯（热gv 在线拉尔·朗万 Gérard Lanvin 饰）和行动大队指挥官德纳尔（西蒙·阿布卡瑞安 Simon Abkarian 饰），两人之间的矛盾已经到了无法调解的白热化程度，他们一位是文森的保护者，一位是他的师父，身陷在恶斗的中心，文森将会作出怎样的选择？

　　这天，小熊维尼（吉姆·库宁斯 Jim Cummings 配音）从睡梦中醒来，发现自己的蜂蜜已经喝御姐很哀伤ed2k光了。于是他走进百亩森林去寻找蜂蜜，路上竟遇到了悲伤的驴子屹耳（巴德·乐凯 Bud Luckey 配音），原来屹耳把自己的尾巴弄丢了。维尼随即找来了跳跳虎、兔子瑞比、猫头鹰、袋鼠妈妈和小国门英雄在线观看豆来帮忙，罗宾提议进行一场比赛，谁先帮屹耳找到了尾巴的代替品，谁将赢得一罐新鲜的蜂蜜。大家便各自使出十八般武艺找来了各种尾巴，然而却没有一条能使屹耳高兴起来。第二天，维尼去找罗宾帮忙，发现门口挂着一张纸条写着“出去一会，马上回来”，识字有限的大伙儿以为罗宾被绑架了，惊恐地组织起营救罗宾的行动，然而此时的维尼，已经快要忍受不了阵阵袭来的饥饿感了……尺寸最大的十大直播平台　　本片根据小熊维尼的原著作者A. A. Milne书中的三个故事改编。

　　本片从证明了费玛最后定理的安德鲁‧怀尔斯 Andrew Wiles开始谈起，描述了 Fermat's Last Theorm 的历史始末，往前回溯来看，1994年正是我在念大学的时候，当时完全没有一位教授在课堂上提到这件事，也许他们认为，一位真正的研究者，自然而然地会被数学吸引，然而对一位不是天才的学生来说，他需要的是老师的指引，引导他走向更高深的专业认知，而指引的道路，就在科普的精神上。　　从费玛最后定理的历史中可以发现，有许多研究成果，都是研究人员燃烧热情，试图提出「有趣」的命题，然后再尝试用逻辑验证。　　费玛最后定理：xn+yn=zn 当 n>2 时，不存在整数解　　1. 1963年 安德鲁‧怀尔斯 Andrew Wiles被埃里克‧坦普尔‧贝尔 Eric Temple Bell 的一本书吸引，「最后问题 The Last Problem」，故事从这里开始。　　2. 毕达哥拉斯 Pythagoras 定理，任一个直角三角形，斜边的平方=另外两边的平方和　　x2+y2=z2　　毕达哥拉斯三元组：毕氏定理的整数解　　3. 费玛 Fermat 在研究丢番图 Diophantus 的「算数」第2卷的问题8时，在页边写下了註记　　「不可能将一个立方数写成两个立方数之和；或者将一个四次幂写成两个四次幂之和；或者，总的来说，不可能将一个高於2次幂，写成两个同样次幂的和。」　　「对这个命题我有一个十分美妙的证明，这里空白太小，写不下。」　　4. 1670年，费玛 Fermat的儿子出版了载有Fermat註记的「丢番图的算数」　　5. 在Fermat的其他註记中，隐含了对 n=4 的证明 => n=8, 12, 16, 20 ... 时无解　　莱昂哈德‧欧拉 Leonhard Euler 证明了 n=3 时无解 => n=6, 9, 12, 15 ... 时无解　　3是质数，现在只要证明费玛最后定理对於所有的质数都成立　　但 欧基里德 证明「存在无穷多个质数」　　6. 1776年 索菲‧热尔曼 针对 (2p+1)的质数，证明了 费玛最后定理 "大概" 无解　　7. 1825年 古斯塔夫‧勒瑞-狄利克雷 和 阿得利昂-玛利埃‧勒让德 延伸热尔曼的证明，证明了 n=5 无解　　8. 1839年 加布里尔‧拉梅 Gabriel Lame 证明了 n=7 无解　　9. 1847年 拉梅 与 奥古斯汀‧路易斯‧科西 Augusti Louis Cauchy 同时宣称已经证明了 费玛最后定理　　最后是刘维尔宣读了 恩斯特‧库默尔 Ernst Kummer 的信，说科西与拉梅的证明，都因为「虚数没有唯一因子分解性质」而失败　　库默尔证明了 费玛最后定理的完整证明 是当时数学方法不可能实现的　　10.1908年 保罗‧沃尔夫斯凯尔 Paul Wolfskehl 补救了库默尔的证明　　这表示 费玛最后定理的完整证明 尚未被解决　　沃尔夫斯凯尔提供了 10万马克 给提供证明的人，期限是到2007年9月13日止　　11.1900年8月8日 大卫‧希尔伯特，提出数学上23个未解决的问题且相信这是迫切需要解决的重要问题　　12.1931年 库特‧哥德尔 不可判定性定理　　第一不可判定性定理：如果公理集合论是相容的，那么存在既不能证明又不能否定的定理。　　=> 完全性是不可能达到的　　第二不可判定性定理：不存在能证明公理系统是相容的构造性过程。　　=> 相容性永远不可能证明　　13.1963年 保罗‧科恩 Paul Cohen 发展了可以检验给定问题是不是不可判定的方法（只适用少数情形）　　证明希尔伯特23个问题中，其中一个「连续统假设」问题是不可判定的，这对於费玛最后定理来说是一大打击　　14.1940年 阿伦‧图灵 Alan Turing 发明破译 Enigma编码 的反转机　　开始有人利用暴力解决方法，要对 费玛最后定理 的n值一个一个加以证明。　　15.1988年 内奥姆‧埃尔基斯 Naom Elkies 对於 Euler 提出的 x4+y4+z4=w4 不存在解这个推想，找到了一个反例　　26824404+153656394+1879604=206156734　　16.1975年 安德鲁‧怀尔斯 Andrew Wiles 师承 约翰‧科次，研究椭圆曲线　　研究椭圆曲线的目的是要算出他们的整数解，这跟费玛最后定理一样　　ex: y2=x3-2 只有一组整数解 52=33-2　　(费玛证明宇宙中指存在一个数26，他是夹在一个平方数与一个立方数中间)　　由於要直接找出椭圆曲线是很困难的，为了简化问题，数学家採用「时鐘运算」方法　　在五格时鐘运算中， 4+2=1　　椭圆方程式 x3-x2=y2+y　　所有可能的解为 (x, y)=(0, 0) (0, 4) (1, 0) (1, 4)，然后可用 E5=4 来代表在五格时鐘运算中，有四个解　　对於椭圆曲线，可写出一个 E序列 E1=1, E2=4, .....　　17.1954年 至村五郎 与 谷山丰 研究具有非同寻常的对称性的 modular form 模型式　　模型式的要素可从1开始标号到无穷（M1, M2, M3, ...）　　每个模型式的 M序列 要素个数 可写成 M1=1 M2=3 .... 这样的范例　　1955年9月 提出模型式的 M序列 可以对应到椭圆曲线的 E序列，两个不同领域的理论突然被连接在一起　　安德列‧韦依 採纳这个想法，「谷山-志村猜想」　　18.朗兰兹提出「朗兰兹纲领」的计画，一个统一化猜想的理论，并开始寻找统一的环链　　19.1984年 格哈德‧弗赖 Gerhard Frey 提出　　(1) 假设费玛最后定理是错的，则 xn+yn=zn 有整数解，则可将方程式转换为y2=x3+(AN-BN)x2-ANBN 这样的椭圆方程式　　(2) 弗赖椭圆方程式太古怪了，以致於无法被模型式化　　(3) 谷山-志村猜想 断言每一个椭圆方程式都可以被模型式化　　(4) 谷山-志村猜想 是错误的　　反过来说　　(1) 如果 谷山-志村猜想 是对的，每一个椭圆方程式都可以被模型式化　　(2) 每一个椭圆方程式都可以被模型式化，则不存在弗赖椭圆方程式　　(3) 如果不存在弗赖椭圆方程式，那么xn+yn=zn 没有整数解　　(4) 费玛最后定理是对的　　20.1986年 肯‧贝里特 证明 弗赖椭圆方程式无法被模型式化　　如果有人能够证明谷山-志村猜想，就表示费玛最后定理也是正确的　　21.1986年 安德鲁‧怀尔斯 Andrew Wiles 开始一个小阴谋，他每隔6个月发表一篇小论文，然后自己独力尝试证明谷山-志村猜想，策略是利用归纳法，加上 埃瓦里斯特‧伽罗瓦 的群论，希望能将E序列以「自然次序」一一对应到M序列　　22.1988年 宫冈洋一 发表利用微分几何学证明谷山-志村猜想，但结果失败　　23.1989年 安德鲁‧怀尔斯 Andrew Wiles 已经将椭圆方程式拆解成无限多项，然后也证明了第一项必定是模型式的第一项，也尝试利用 依娃沙娃 Iwasawa 理论，但结果失败　　24.1992年 修改 科利瓦金-弗莱契 方法，对所有分类后的椭圆方程式都奏效　　25.1993年 寻求同事 尼克‧凯兹 Nick Katz 的协助，开始对验证证明　　26.1993年5月 「L-函数和算术」会议，安德鲁‧怀尔斯 Andrew Wiles 发表谷山-志村猜想的证明　　27.1993年9月 尼克‧凯兹 Nick Katz 发现一个重大缺陷　　安德鲁‧怀尔斯 Andrew Wiles 又开始隐居，尝试独力解决缺陷，他不希望在这时候公布证明，让其他人分享完成证明的甜美果实　　28.安德鲁‧怀尔斯 Andrew Wiles 在接近放弃的边缘，在彼得‧萨纳克的建议下，找到理查德‧泰勒的协助　　29.1994年9月19日 发现结合 依娃沙娃 Iwasawa 理论与 科利瓦金-弗莱契 方法就能够完全解决问题　　30.「谷山-志村猜想」被证明了，故得证「费玛最后定理」　　ii　　费马大定理　　300多年以前，法国数学家费马在一本书的空白处写下了一个定理：“设n是大于2的正整数，则不定方程xn+yn=zn没有非零整数解”。　　费马宣称他发现了这个定理的一个真正奇妙的证明，但因书上空白太小，他写不下他的证明。300多年过去了，不知有多少专业数学家和业余数学爱好者绞尽脑汁企图证明它，但不是无功而返就是进展甚微。这就是纯数学中最着名的定理—费马大定理。　　费马(1601年～1665年)是一位具有传奇色彩的数学家，他最初学习法律并以当律师谋生，后来成为议会议员，数学只不过是他的业余爱好，只能利用闲暇来研究。虽然年近30才认真注意数学，但费马对数论和微积分做出了第一流的贡献。他与笛卡儿几乎同时创立了解析几何，同时又是17世纪兴起的概率论的探索者之一。费马特别爱好数论，提出了许多定理，但费马只对其中一个定理给出了证明要点，其他定理除一个被证明是错的，一个未被证明外，其余的陆续被后来的数学家所证实。这唯一未被证明的定理就是上面所说的费马大定理，因为是最后一个未被证明对或错的定理，所以又称为费马最后定理。　　费马大定理虽然至今仍没有完全被证明，但已经有了很大进展，特别是最近几十年，进展更快。1976年瓦格斯塔夫证明了对小于105的素数费马大定理都成立。1983年一位年轻的德国数学家法尔廷斯证明了不定方程xn+yn=zn只能有有限多组解，他的突出贡献使他在1986年获得了数学界的最高奖之一费尔兹奖。1993年英国数学家威尔斯宣布证明了费马大定理，但随后发现了证明中的一个漏洞并作了修正。虽然威尔斯证明费马大定理还没有得到数学界的一致公认，但大多数数学家认为他证明的思路是正确的。毫无疑问，这使人们看到了希望。　　为了寻求费马大定理的解答，三个多世纪以来，一代又一代的数学家们前赴后继，却壮志未酬。1995年，美国普林斯顿大学的安德鲁·怀尔斯教授经过8年的孤军奋战，用13　　0页长的篇幅证明了费马大定理。怀尔斯成为整个数学界的英雄。　　费马大定理提出的问题非常简单，它是用一个每个中学生都熟悉的数学定理——毕达　　哥拉斯定理——来表达的。2000多年前诞生的毕达哥拉斯定理说：在一个直角三角形中，　　斜边的平方等于两直角边的平方之和。即X2＋Y2=Z2。大约在公元1637年前后 ，当费马在　　研究毕达哥拉斯方程时，他写下一个方程，非常类似于毕达哥拉斯方程：Xn＋Yn=Zn,当n　　大于2时，这个方程没有任何整数解。费马在《算术》这本书的靠近问题8的页边处记下这　　个结论的同时又写下一个附加的评注：“对此，我确信已发现一个美妙的证法，这里的空　　白太小，写不下。”这就是数学史上着名的费马大定理或称费马最后的定理。费马制造了　　一个数学史上最深奥的谜。　　大问题　　在物理学、化学或生物学中，还没有任何问题可以叙述得如此简单和清晰，却长久不　　解。E·T·贝尔(Eric Temple Bell)在他的《大问题》(The Last Problem)一书中写到，　　文明世界也许在费马大定理得以解决之前就已走到了尽头。证明费马大定理成为数论中最　　值得为之奋斗的事。　　安德鲁·怀尔斯1953年出生在英国剑桥，父亲是一位工程学教授。少年时代的怀尔斯　　已着迷于数学了。他在后来的回忆中写到：“在学校里我喜欢做题目，我把它们带回家，　　编写成我自己的新题目。不过我以前找到的最好的题目是在我们社区的图书馆里发现的。　　”一天，小怀尔斯在弥尔顿街上的图书馆看见了一本书，这本书只有一个问题而没有解答　　,怀尔斯被吸引住了。　　这就是E·T·贝尔写的《大问题》。它叙述了费马大定理的历史，这个定理让一个又　　一个的数学家望而生畏，在长达300多年的时间里没有人能解决它。怀尔斯30多年后回忆　　起被引向费马大定理时的感觉：“它看上去如此简单，但历史上所有的大数学家都未能解　　决它。这里正摆着我——一个10岁的孩子——能理解的问题，从那个时刻起，我知道我永　　远不会放弃它。我必须解决它。”　　怀尔斯1974年从牛津大学的Merton学院获得数学学士学位，之后进入剑桥大学Clare　　学院做博士。在研究生阶段，怀尔斯并没有从事费马大定理研究。他说：“研究费马可能　　带来的问题是：你花费了多年的时间而最终一事无成。我的导师约翰·科茨(John Coate　　s)正在研究椭圆曲线的Iwasawa理论，我开始跟随他工作。” 科茨说：“我记得一位同事　　告诉我，他有一个非常好的、刚完成数学学士荣誉学位第三部考试的学生，他催促我收其　　为学生。我非常荣幸有安德鲁这样的学生。即使从对研究生的要求来看，他也有很深刻的　　思想，非常清楚他将是一个做大事情的数学家。当然，任何研究生在那个阶段直接开始研　　究费马大定理是不可能的，即使对资历很深的数学家来说，它也太困难了。”科茨的责任　　是为怀尔斯找到某种至少能使他在今后三年里有兴趣去研究的问题。他说：“我认为研究　　生导师能为学生做的一切就是设法把他推向一个富有成果的方向。当然，不能保证它一定　　是一个富有成果的研究方向，但是也许年长的数学家在这个过程中能做的一件事是使用他　　的常识、他对好领域的直觉。然后，学生能在这个方向上有多大成绩就是他自己的事了。　　”　　科茨决定怀尔斯应该研究数学中称为椭圆曲线的领域。这个决定成为怀尔斯职业生涯中的　　一个转折点，椭圆方程的研究是他实现梦想的工具。　　孤独的战士　　1980年怀尔斯在剑桥大学取得博士学位后来到了美国普林斯顿大学，并成为这所大学　　的教授。在科茨的指导下，怀尔斯或许比世界上其他人都更懂得椭圆方程，他已经成为一　　个着名的数论学家，但他清楚地意识到，即使以他广博的基础知识和数学修养，证明费马　　大定理的任务也是极为艰巨的。　　在怀尔斯的费马大定理的证明中，核心是证明“谷山－志村猜想”，该猜想在两个非　　常不同的数学领域间建立了一座新的桥梁。“那是1986年夏末的一个傍晚，我正在一个朋　　友家中啜饮冰茶。谈话间他随意告诉我，肯·里贝特已经证明了谷山－志村猜想与费马大　　定理间的联系。我感到极大的震动。我记得那个时刻，那个改变我生命历程的时刻，因为　　这意味着为了证明费马大定理，我必须做的一切就是证明谷山－志村猜想……我十分清楚　　我应该回家去研究谷山－志村猜想。”怀尔斯望见了一条实现他童年梦想的道路。　　20世纪初，有人问伟大的数学家大卫·希尔伯特为什么不去尝试证明费马大定理，他　　回答说：“在开始着手之前，我必须用3年的时间作深入的研究，而我没有那么多的时间　　浪费在一件可能会失败的事情上。”怀尔斯知道，为了找到证明，他必须全身心地投入到　　这个问题中，但是与希尔伯特不一样，他愿意冒这个风险。　　怀尔斯作了一个重大的决定：要完全独立和保密地进行研究。他说：“我意识到与费　　马大定理有关的任何事情都会引起太多人的兴趣。你确实不可能很多年都使自己精力集中　　，除非你的专心不被他人分散，而这一点会因旁观者太多而做不到。”怀尔斯放弃了所有　　与证明费马大定理无直接关系的工作，任何时候只要可能他就回到家里工作，在家里的顶　　楼书房里他开始了通过谷山－志村猜想来证明费马大定理的战斗。　　这是一场长达7年的持久战，这期间只有他的妻子知道他在证明费马大定理。　　欢呼与等待　　经过7年的努力，怀尔斯完成了谷山－志村猜想的证明。作为一个结果，他也证明了　　费马大定理。现在是向世界公布的时候了。1993年6月底，有一个重要的会议要在剑桥大　　学的牛顿研究所举行。怀尔斯决定利用这个机会向一群杰出的听众宣布他的工作。他选择　　在牛顿研究所宣布的另外一个主要原因是剑桥是他的家乡，他曾经是那里的一名研究生。　　1993年6月23日，牛顿研究所举行了20世纪最重要的一次数学讲座。两百名数学家聆　　听了这一演讲，但他们之中只有四分之一的人完全懂得黑板上的希腊字母和代数式所表达　　的意思。其余的人来这里是为了见证他们所期待的一个真正具有意义的时刻。演讲者是安　　德鲁·怀尔斯。怀尔斯回忆起演讲最后时刻的情景：“虽然新闻界已经刮起有关演讲的风　　声，很幸运他们没有来听演讲。但是听众中有人拍摄了演讲结束时的镜头，研究所所长肯　　定事先就准备了一瓶香槟酒。当我宣读证明时，会场上保持着特别庄重的寂静，当我写完　　费马大定理的证明时，我说：‘我想我就在这里结束’，会场上爆发出一阵持久的鼓掌声　　。”　　《纽约时报》在头版以《终于欢呼“我发现了!”，久远的数学之谜获解》为题报道　　费马大定理被证明的消息。一夜之间，怀尔斯成为世界上最着名的数学家，也是唯一的数　　学家。《人物》杂志将怀尔斯与戴安娜王妃一起列为“本年度25位最具魅力者”。最有创　　意的赞美来自一家国际制衣大公司，他们邀请这位温文尔雅的天才作他们新系列男装的模　　特。　　当怀尔斯成为媒体报道的中心时，认真核对这个证明的工作也在进行。科学的程序要　　求任何数学家将完整的手稿送交一个有声望的刊物，然后这个刊物的编辑将它送交一组审　　稿人，审稿人的职责是进行逐行的审查证明。怀尔斯将手稿投到《数学发明》，整整一个　　夏天他焦急地等待审稿人的意见，并祈求能得到他们的祝福。可是，证明的一个缺陷被发　　现了。　　我的心灵归于平静　　由于怀尔斯的论文涉及到大量的数学方法，编辑巴里·梅休尔决定不像通常那样指定　　2－3个审稿人，而是6个审稿人。200页的证明被分成6章，每位审稿人负责其中一章。　　怀尔斯在此期间中断了他的工作，以处理审稿人在电子邮件中提出的问题，他自信这　　些问题不会给他造成很大的麻烦。尼克·凯兹负责审查第3章，1993年8月23日，他发现了　　证明中的一个小缺陷。数学的绝对主义要求怀尔斯无可怀疑地证明他的方法中的每一步都　　行得通。怀尔斯以为这又是一个小问题，补救的办法可能就在近旁，可是6个多月过去了　　，错误仍未改正，怀尔斯面临绝境，他准备承认失败。他向同事彼得·萨克说明自己的情　　况，萨克向他暗示困难的一部分在于他缺少一个能够和他讨论问题并且可信赖的人。经过　　长时间的考虑后，怀尔斯决定邀请剑桥大学的讲师理查德·泰勒到普林斯顿和他一起工作　　。　　泰勒1994年1月份到普林斯顿，可是到了9月，依然没有结果，他们准备放弃了。泰勒　　鼓励他们再坚持一个月。怀尔斯决定在9月底作最后一次检查。9月19日，一个星期一的早　　晨，怀尔斯发现了问题的答案，他叙述了这一时刻：“突然间，不可思议地，我有了一个　　难以置信的发现。这是我的事业中最重要的时刻，我不会再有这样的经历……它的美是如　　此地难以形容；它又是如此简单和优美。20多分钟的时间我呆望它不敢相信。然后白天我　　到系里转了一圈，又回到桌子旁看看它是否还在——它还在那里。”　　这是少年时代的梦想和8年潜心努力的终极，怀尔斯终于向世界证明了他的才能。世　　界不再怀疑这一次的证明了。这两篇论文总共有130页，是历史上核查得最彻底的数学稿　　件，它们发表在1995年5月的《数学年刊》上。怀尔斯再一次出现在《纽约时报》的头版　　上，标题是《数学家称经典之谜已解决》。约翰·科茨说：“用数学的术语来说，这个最　　终的证明可与分裂原子或发现DNA的结构相比，对费马大定理的证明是人类智力活动的一　　曲凯歌，同时，不能忽视的事实是它一下子就使数学发生了革命性的变化。对我说来，安　　德鲁成果的美和魅力在于它是走向代数数论的巨大的一步。”　　声望和荣誉纷至沓来。1995年，怀尔斯获得瑞典皇家学会颁发的Schock数学奖，199　　6年，他获得沃尔夫奖，并当选为美国科学院外籍院士。　　怀尔斯说：“……再没有别的问题能像费马大定理一样对我有同样的意义。我拥有如　　此少有的特权，在我的成年时期实现我童年的梦想……那段特殊漫长的探索已经结束了，　　我的心已归于平静。”　　费马大定理只有在相对数学理论的建立之后，才会得到最满意的答案。相对数学理论没有完成之前，谈这个问题是无力地.因为人们对数量和自身的认识，还没有达到一定的高度.　　iii　　费马大定理与怀尔斯的因果律-美国公众广播网对怀尔斯的专访　　358年的难解之谜　　数学爱好者费马提出的这个问题非常简单，它用一个每个中学生都熟悉的数学定理——毕达哥拉斯定理来表达。2000多年前诞生的毕达哥拉斯定理说：在一个直角三角形中，斜边的平方等于两个直角边的平方之和。即X2+Y2=Z2。大约在公元1637年前后 ，当费马在研究毕达哥拉斯方程时，他在《算术》这本书靠近问题8的页边处写下了这段文字：“设n是大于2的正整数，则不定方程xn+yn=zn没有非整数解，对此，我确信已发现一个美妙的证法，但这里的空白太小，写不下。”费马习惯在页边写下猜想，费马大定理是其中困扰数学家们时间最长的，所以被称为Fermat’s Last Theorem（费马最后的定理）——公认为有史以来最着名的数学猜想。　　在畅销书作家西蒙·辛格（Simon Singh）的笔下，这段神秘留言引发的长达358年的猎逐充满了惊险、悬疑、绝望和狂喜。这段历史先后涉及到最多产的数学大师欧拉、最伟大的数学家高斯、由业余转为职业数学家的柯西、英年早逝的天才伽罗瓦、理论兼试验大师库默尔和被誉为“法国历史上知识最为高深的女性”的苏菲·姬尔曼……法国数学天才伽罗瓦的遗言、日本数学界的明日之星谷山丰的神秘自杀、德国数学爱好者保罗·沃尔夫斯凯尔最后一刻的舍死求生等等，都仿佛是冥冥间上帝导演的宏大戏剧中的一幕，为最后谜底的解开埋下伏笔。终于，普林斯顿的怀尔斯出现了。他找到谜底，把这出戏推向高潮并戛然而止，留下一段耐人回味的传奇。　　对怀尔斯而言，证明费马大定理不仅是破译一个难解之谜，更是去实现一个儿时的梦想。“我10岁时在图书馆找到一本数学书，告诉我有这么一个问题，300多年前就已经有人解决了它，但却没有人看到过它的证明，也无人确信是否有这个证明，从那以后，人们就不断地求证。这是一个10岁小孩就能明白的问题，然后历史上诸多伟大的数学家们却不能解答。于是从那时起，我就试过解决它，这个问题就是费马大定理。”　　怀尔斯于1970年先后在牛津大学和剑桥大学获得数学学士和数学博士学位。“我进入剑桥时，我真正把费马大定理搁在一边了。这不是因为我忘了它，而是我认识到我们所掌握的用来攻克它的全部技术已经反复使用了130年。而这些技术似乎没有触及问题根本。”因为担心耗费太多时间而一无所获，他“暂时放下了”对费马大定理的思索，开始研究椭圆曲线理论——这个看似与证明费马大定理不相关的理论后来却成为他实现梦想的工具。　　时间回溯至20世纪60年代，普林斯顿数学家朗兰兹提出了一个大胆的猜想：所有主要数学领域之间原本就存在着的统一的链接。如果这个猜想被证实，意味着在某个数学领域中无法解答的任何问题都有可能通过这种链接被转换成另一个领域中相应的问题——可以被一整套新方案解决的问题。而如果在另一个领域内仍然难以找到答案，那么可以把问题再转换到下一个数学领域中……直到它被解决为止。根据朗兰兹纲领，有一天，数学家们将能够解决曾经是最深奥最难对付的问题——“办法是领着这些问题周游数学王国的各个风景胜地”。这个纲领为饱受哥德尔不完备定理打击的费马大定理证明者们指明了救赎之路——根据不完备定理，费马大定理是不可证明的。　　怀尔斯后来正是依赖于这个纲领才得以证明费马大定理的：他的证明——不同于任何前人的尝试——是现代数学诸多分支（椭圆曲线论，模形式理论，伽罗华表示理论等等)综合发挥作用的结果。20世纪50年代由两位日本数学家（谷山丰和志村五郎）提出的谷山—志村猜想（Taniyama-Shimura conjecture）暗示：椭圆方程与模形式两个截然不同的数学岛屿间隐藏着一座沟通的桥梁。随后在1984年，德国数学家格哈德·费赖（Gerhard Frey）给出了如下猜想：假如谷山—志村猜想成立，则费马大定理为真。这个猜想紧接着在1986年被肯·里贝特（Ken Ribet）证明。从此，费马大定理不可摆脱地与谷山—志村猜想链接在一起：如果有人能证明谷山—志村猜想（即“每一个椭圆方程都可以模形式化”），那么就证明了费马大定理。　　“人类智力活动的一曲凯歌”　　怀尔斯诡秘的行踪让普林斯顿的着名数学家同事们困惑。彼得·萨奈克（Peter Sarnak）回忆说：“ 我常常奇怪怀尔斯在做些什么？……他总是静悄悄的，也许他已经‘黔驴技穷’了。”尼克·凯兹则感叹到：“一点暗示都没有！”对于这次惊天“大预谋”，肯·里比特（Ken Ribet)曾评价说：“这可能是我平生来见过的唯一例子，在如此长的时间里没有泄露任何有关工作的信息。这是空前的。　　1993年晚春，在经过反复的试错和绞尽脑汁的演算，怀尔斯终于完成了谷山—志村猜想的证明。作为一个结果，他也证明了费马大定理。彼得·萨奈克是最早得知此消息的人之一，“我目瞪口呆、异常激动、情绪失常……我记得当晚我失眠了”。　　同年6月，怀尔斯决定在剑桥大学的大型系列讲座上宣布这一证明。 “讲座气氛很热烈，有很多数学界重要人物到场，当大家终于明白已经离证明费马大定理一步之遥时，空气中充满了紧张。” 肯·里比特回忆说。巴里·马佐尔（Barry Mazur）永远也忘不了那一刻：“我之前从未看到过如此精彩的讲座，充满了美妙的、闻所未闻的新思想，还有戏剧性的铺垫，充满悬念，直到最后到达高潮。”当怀尔斯在讲座结尾宣布他证明了费马大定理时，他成了全世界媒体的焦点。《纽约时报》在头版以《终于欢呼“我发现了!”久远的数学之谜获解》（“At Last Shout of ‘Eureka!’ in Age-Old Math Mystery”）为题报道费马大定理被证明的消息。一夜之间，怀尔斯成为世界上唯一的数学家。《人物》杂志将怀尔斯与戴安娜王妃一起列为“本年度25位最具魅力者”。　　与此同时，认真核对这个证明的工作也在进行。遗憾的是，如同这之前的“费马大定理终结者”一样，他的证明是有缺陷的。怀尔斯现在不得不在巨大的压力之下修正错误，其间数度感到绝望。John Conway曾在美国公众广播网（PBS）的访谈中说: “当时我们其他人（怀尔斯的同事）的行为有点像‘苏联政体研究者’，都想知道他的想法和修正错误的进展，但没有人开口问他。所以，某人会说，‘我今天早上看到怀尔斯了。’‘他露出笑容了吗？’‘他倒是有微笑，但看起来并不高兴。’”　　撑到1994年9月时，怀尔斯准备放弃了。但他临时邀请的研究搭档泰勒鼓励他再坚持一个月。就在截止日到来之前两周， 9月19日 ，一个星期一的早晨，怀尔斯发现了问题的答案，他叙述了这一时刻：“突然间，不可思议地，我发现了它……它美得难以形容，简单而优雅。我对着它发了20多分钟呆。然后我到系里转了一圈，又回到桌子旁看看它是否还在那里——它确实还在那里。”　　怀尔斯的证明为他赢得了最慷慨的褒扬，其中最具代表性的是他在剑桥时的导师、着名数学家约翰·科茨的评价：“它（证明）是人类智力活动的一曲凯歌”。　　一场旷日持久的猎逐就此结束，从此费马大定理与安德鲁·怀尔斯的名字紧紧地被绑在了一起，提到一个就不得不提到另外一个。这是费马大定理与安德鲁·怀尔斯的因果律。　　历时八年的最终证明　　在怀尔斯不多的接受媒体采访中，美国公众广播网（PBS）NOVA节目对怀尔斯的专访相当精彩有趣，本文节选部分以飨读者。　　七年孤独　　NOVA：通常人们通过团队来获得工作上的支持，那么当你碰壁时是怎么解决问题的呢？　　怀尔斯：当我被卡住时我会沿着湖边散散步，散步的好处是使你会处于放松状态，同时你的潜意识却在继续工作。通常遇到困扰时你并不需要书桌，而且我随时把笔纸带上，一旦有好主意我会找个长椅坐下来打草稿……　　NOVA：这七年一定交织着自我怀疑与成功……你不可能绝对有把握证明。　　怀尔斯：我确实相信自己在正确的轨道上，但那并不意味着我一定能达到目标——也许仅仅因为解决难题的方法超出现有的数学，也许我需要的方法下个世纪也不会出现。所以即便我在正确的轨道上，我却可能生活在错误的世纪。　　NOVA：最终在1993年，你取得了突破。　　怀尔斯：对，那是个5月末的早上。Nada，我的太太，和孩子们出去了。我坐在书桌前思考最后的步骤，不经意间看到了一篇论文，上面的一行字引起了我的注意。它提到了一个19世纪的数学结构，我霎时意识到这就是我该用的。我不停地工作，忘记下楼午饭，到下午三四点时我确信已经证明了费马大定理，然后下楼。Nada很吃惊，以为我这时才回家，我告诉她，我解决了费马大定理。　　最后的修正　　NOVA：《纽约时报》在头版以《终于欢呼“我发现了!”，久远的数学之谜获解》，但他们并不知道这个证明中有个错误。　　怀尔斯：那是个存在于关键推导中的错误，但它如此微妙以至于我忽略了。它很抽象，我无法用简单的语言描述，就算是数学家也需要研习两三个月才能弄懂。　　NOVA：后来你邀请剑桥的数学家理查德·泰勒来协助工作，并在1994年修正了这个最后的错误。问题是，你的证明和费马的证明是同一个吗？　　怀尔斯：不可能。这个证明有150页长，用的是20世纪的方法，在费马时代还不存在。　　NOVA：那就是说费马的最初证明还在某个未被发现的角落？　　怀尔斯：我不相信他有证明。我觉得他说已经找到解答了是在哄自己。这个难题对业余爱好者如此特别在于它可能被17世纪的数学证明，尽管可能性极其微小。　　NOVA：所以也许还有数学家追寻这最初的证明。你该怎么办呢？　　怀尔斯：对我来说都一样，费马是我童年的热望。我会再试其他问题……证明了它我有一丝伤感，它已经和我们一起这么久了……人们对我说“你把我的问题夺走了”，我能带给他们其他的东西吗？我感觉到有责任。我希望通过解决这个问题带来的兴奋可以激励青年数学家们解决其他许许多多的难题。　　iv　　谷山-志村定理(Taniyama-Shimura theorem)建立了椭圆曲线(代数几何的对象)和模形式(某种数论中用到的周期性全纯函数)之间的重要联系。虽然名字是从谷山-志村猜想而来,定理的证明是由安德鲁·怀尔斯, Christophe Breuil, Brian Conrad, Fred Diamond,和Richard Taylor完成.　　若p是一个质数而E是一个Q(有理数域)上的一个椭圆曲线，我们可以简化定义E的方程模p;除了有限个p值，我们会得到有np个元素的有限域Fp上的一个椭圆曲线。然后考虑如下序列　　ap = np − p,　　这是椭圆曲线E的重要的不变量。从傅里叶变换，每个模形式也会产生一个数列。一个其序列和从模形式得到的序列相同的椭圆曲线叫做模的。 谷山-志村定说:　　"所有Q上的椭圆曲线是模的"。　　该定理在1955年9月由谷山丰提出猜想。到1957年为止，他和志村五郎一起改进了严格性。谷山于1958年自杀身亡。在1960年代，它和统一数学中的猜想Langlands纲领联系了起来，并是关键的组成部分。猜想由André Weil于1970年代重新提起并得到推广，Weil的名字有一段时间和它联系在一起。尽管有明显的用处，这个问题的深度在后来的发展之前并未被人们所感觉到。　　在1980年代当Gerhard Freay建议谷山-志村猜想(那时还是猜想)蕴含着费马最后定理的时候，它吸引到了不少注意力。他通过试图表明费尔马大定理的任何范例会导致一个非模的椭圆曲线来做到这一点。Ken Ribet后来证明了这一结果。在1995年，Andrew Wiles和Richard Taylor证明了谷山-志村定理的一个特殊情况(半稳定椭圆曲线的情况)，这个特殊情况足以证明费尔马大定理。　　完整的证明最后于1999年由Breuil,Conrad,Diamond,和Taylor作出，他们在Wiles的基础上，一块一块的逐步证明剩下的情况直到全部完成。　　数论中类似于费尔马最后定理得几个定理可以从谷山-志村定理得到。例如:没有立方可以写成两个互质n次幂的和, n ≥ 3. (n = 3的情况已为欧拉所知)　　在1996年三月，Wiles和Robert Langlands分享了沃尔夫奖。虽然他们都没有完成给予他们这个成就的定理的完整形式，他们还是被认为对最终完成的嘟嘟嘟影视在线观看证明有着决定性影响。

　　故事发生致命弯道2电影在二十世纪初的墨西哥革命中。一辆长途马车里，高贵的先生女士们对一位沉默寡言的农民大放厥词，然而突然农民摇身一变，显出家庭式匪帮头目胡安（Rod Steiger 饰）的真面目。胡安打劫后路遇爱尔兰革命军爆破专家约翰（James Coburn 饰），后者的爆破能力令抢劫忘忧草在线播放www中国梅萨维德银行如探囊取物，于是胡安苦苦尾随，不经意间却卷入了配合维拉革命军的梅萨维德暴动。胡安如愿与约翰搭档洗劫银行，但他所有的收获却是解放150名政治犯人。　　政府军上校刚特率军镇压革命，胡安与革命队伍付出了惨痛的代价。在逆境中，约翰与胡安产生了真正的革命情谊，二人在前往美国的路上折返阻击刚特上校，当约翰中弹之时，这位老战士看到了昔日在爱尔兰的温馨场景……本片获1972年意大利大港剧网在线观看卫奖最佳导演奖。

　　炎热的夏天过去，枝上的树叶慢慢转成红色。中央公园内，松鼠、浣熊们发现过冬的坚果根本不够用，这群小动物可能面临一场前所未有的饥荒。松鼠塞利（威尔·阿奈特 Will Arnett 配音）和安迪（凯瑟琳·海格尔 Katherine Heigl 配音）奉命前去寻找坚果，它们计划打劫一辆坚果车，谁知却造成了一场大混乱，还导致好不容易的手的坚果毁于大火。在此之后，塞利遭到流放，只有他的老鼠朋友巴蒂（Robert Tinkler 配音）自始至终跟着他。另一方面，安迪则和自我感觉良好的同伴格里森踏上寻找坚果的征途。最终，安迪和塞利在一座库藏丰富的坚果店重逢，而那里的幕后老板竟然是一个臭名昭著、穷凶极恶的罪犯。　　螳螂捕蝉，黄雀在后，犯罪分子策划新的劫我是特种兵第三部案同时，却不知有一群小动物正准备打劫他们……

　　稳定的心态，精妙的手法，杀人于无形，这是一个顶尖杀手的必备特质。亚瑟（杰森•斯坦森Jason Statham 饰）入行多年，在自己以前的搭档哈里（唐纳德•萨瑟兰Donald Sutherland 饰）的帮助久青草视频免费视频下，已经成为一个出色的杀人机器。亚瑟接到一项新任务，暗杀对象是哈 里。虽然亚瑟不忍下手，但在清楚的得知哈里难逃一死之后，最终还是决定亲自送哈里一程。哈里的儿子史蒂夫（本•福斯特 Ben Foster 饰）为了替父报仇，决意要跟随亚瑟学习。在亚瑟的训练下，史蒂夫逐渐掌握了作为一个机械师所必备的技能，与亚瑟合作完成一项又一项暗杀任务。虽然亚瑟从未告诉史蒂夫杀害哈里的凶手，但史蒂夫还是知道了其父被害为亚瑟所为，复仇的火焰在史蒂夫心中逐渐升腾……　　本片翻拍自1972年的同名电影（译作《龙虎铁金钢》），投资约4000万美元。

　　退休炸弹专家佩恩（丹尼斯•霍珀 Dennis Hopper 饰）因不满政府的退休政策，产生了报复社会的念头。他先是在电梯里安装炸弹，www hhh258 com劫持人质勒索100万美元赎金，但被特警杰克（基努•李维斯 Keanu Reeves 饰）拆除了炸弹，救出了人质。佩恩趁乱逃脱。　　一计不成，佩恩并没有放弃，他继续他疯狂的计划。这次他炸毁了一辆公车，并在另一辆公车上安装了炸弹，只要该公车的时速超过了50英里就不能再减速，否则就会引起爆炸。当杰克赶上这辆公车时，公车已经满载乘客行驶在高速公路上，时速也早已过了50英里。　　杰克是俗称的“胆生毛”，他冒险上了公车，和佩恩之间的我的好妈妈5在线观看版生死时速开始了。

　　萨宾（碧翠丝·罗曼德 Béatrice Romand 饰）交往过几个男人，但遗憾的是他们均是有妇之夫，这让萨宾感到十分不悦。某一天，萨宾忽然告诉她的好友克拉丽丝（阿丽尔·朵巴丝勒 Arielle Dombasle 饰）自己决定结婚，可她连个男朋友都还没有呢！在克拉丽丝的介绍下，萨宾结识了名为艾德蒙（安德烈·杜索里埃 André D异星战场3dussollier 饰）的男子，艾德蒙是一名律师，年纪轻轻事业有成，萨宾认定了艾德蒙是她未来规划中的完美丈夫。　　就这样，萨宾和艾德蒙展开了周旋，她十分渴望得到艾德蒙的青睐，却又不愿意做主动的那一方。对于萨宾的亲近，艾德蒙不主动不拒绝，直到他开始以种种借口避免和萨宾通话和见面，萨宾才发现，自己一厢情愿的举动是多么的天真。

　　所有人都以为，艾米（米拉·库妮丝 Mila Kunis 饰）拥有着幸福美满的婚姻生活——恩爱的丈夫，乖巧的孩子，优渥的生活条件，但只有艾米自己知道，为了维系这看似光鲜的表象，她的内心早已经精疲力尽。丈夫把所有的家务事都一股脑的甩在她的头上，在处美女的比理这些琐事的同时，艾米还必须兼顾着去讨好她周围其他的妈妈们。　　终于有一天，艾米再也受不了她的生活了，她离开了家庭，抛弃了丈夫和孩子，带着闺蜜琪琪（克里斯汀·贝尔 Kristen Bell 饰）和卡拉（凯瑟琳·哈恩 Kathryn Hahn 饰），两名同样受到生活疯狂压榨的家庭主妇，三人踏上了一条疯狂的狂欢之路。

太平间闹鬼事件2在线观看完整版　　这部昔日的CBS旗舰剧集已经失去了一个好汉（Charlie Sheen被开除，Charlie Harper也随之死亡），现在又将失去半个好汉——因为种种原因（如果你相信CBS官方所说的「他要读大学」那你就太天真了），Angus T. Jones不再是该剧的常规演员，他的名字也将从片忘忧草资源在线观看免费观看头字幕中彻底抹除。

　　CJAPANBABES日本老师BS宣布续订《得得咋好汉两个半》。

　　他是花花公子的典型，对女人很有手段，做广告配乐的，几乎不工作，却能赚大把的钱，穿梭不断的美女和音乐就是他生活的主题。可是alan的出现打破豆奶app软件下载安装了他单身汉的快乐生活。　　　　Alan被老婆赶了出来，和兄弟Charlie住在一起。工作是指压按摩师。他是一个有责任心，对妻子百依百顺的好丈夫，但是唧唧歪歪的性格，粘粘糊糊的脾气，让人想到唐僧。一直试图和妻子和好，分居了还老回去干家务，她却宣布自己是女同性恋。　　　　一个儿子Jake，胖胖的很可爱，虽然年纪小小，也有点好色，无论多少东西都吃得下。大智若愚的性格，让他成为本剧的大亮点，一点不输给两个成年的男主角。和蜡笔小心有得一拼。　　　　值得一提的是 几个配角，让兄弟两个对女人产生阴影的魔鬼老妈，刻薄的前妻，拽得要死的清洁女佣，还有和Charlie共渡一夜之后就跟踪了他两三年的邻居Rose

　　本剧是美国CBS电视台的金牌喜剧，目前已获得1项艾美奖，7项其他各类大奖，包括2项金球奖提名在内的操肥臀18项各类提名。　　Charlie是一个潇洒自由的单身汉，但正面临离婚危机的兄弟Alan带着儿子Jake的突然来访完全打乱了Charlie悠然自得的生活，三个男人一台戏，这下可有得乐了，在去年全美情景喜剧收视一片低迷的大背景下《Two and a Half Men》强势出击，夺下该类剧集收视全国第二的骄人战果，不得不让人刮目相看。　　两个半男人是因为小Jack也很好色啦，年纪太小，只能算半个。　　主角是兄弟两个charlie sheen--经典电影华尔街，野战排，电视the spin city政界小人物的男主角，the west wing白宫风云总统扮演者Martin sheen(电影现代启示录) 的儿子，007女郎丹尼斯里查兹的前夫，离婚中。　　他是花花公子的典型，对女人很有手段，做广告配乐的，几乎不工作，却能赚大把的钱，穿梭不断的美女和音乐就是他生活的主题。可是alan的出现打破了他单身汉的快乐生活。　　Alan被老婆赶了出来，和兄弟Charlie住在一起。工作是指压按摩师。他是一个有责任心，对妻子百依百顺的好丈夫，但是唧唧歪歪的性格，粘粘糊糊的脾气，让人想到唐僧。一直试图和妻子和好，分居了还老回去乾家务，她却宣布自己是女同性恋。　　一个儿子Jake，胖胖的很可爱，虽然年纪小小，也有点好色，无论多少东西都吃得下。大智若愚的性格，让他成为本剧的大亮点，一点不输给两个成年的男主角。和蜡笔小心有得一拼。　　值得一提的是 几个配角，让兄弟两个对女人产生阴影的魔鬼老妈，刻薄的前妻，拽得要死的清洁女佣，还有和Charlie共渡一夜之后就跟踪了他两三年的邻居Ro死神3se　　故事就在这三个主角和他们周围的女人中发生。by:m.yakubd.cc

　　本剧是美国CBS电视台的金牌喜剧，目前已获得1项艾美奖，7项其他各类大奖，包括2项金球奖提名在内的18项各类提名。　　Charlie是一个潇洒自由的单身汉，但离婚后被前妻剥夺了几乎一切财产的弟弟Alan带着儿子Jake的突然来访完全打乱了妈妈的朋友16中语版在看Charlie悠然自得的生活，三个男人一台戏，这下可有得乐了，在全美情景喜剧收视一片低迷的大背景下《Two and aHalfMen》强势出击，夺下该类剧集收视全国第二的骄人战果，不得不让人刮目相看。　　好汉两个半的“半个：是因为Jake年纪太小，只能算半个。　　主角是兄弟俩，哥哥Charlie是典型的花花公子，非常有女人缘，职业是给广告配乐，很少工作，却能赚大把的钱，穿梭不断的美女和音乐就是他生活的全部。可是Alan的出现打破了他平静的单身汉生活。　　Alan离婚后被前妻赶了出来，和兄弟Charlie住在一起。职业是指压按摩师。他的事业一直停滞不前，很喜欢被人称为“医生”，尽管他算不上…　　Alan的儿子Jake，胖胖的很可爱，虽然年纪全职高手2季动漫免费观看小小，也有点好色，无论多少东西都吃得下。大智若愚的性格，让他成为本剧的一大亮点，一点不输给两个成年的男主角。和蜡笔小新有得拼。　　几个黄金配角同样不可忽视，让兄弟两个对女人产生阴影的魔鬼老妈，刻薄的前妻，拽得要死的清洁女佣，还有和Charlie共渡一夜之后就跟踪了他两三年的邻居Rose。　　故事就在这三个主角和他们周围的女人中发生,很含羞草实验所免费网站进入多的客串嘉宾哦，有Sing in the rain里面的女演员，绝望主妇苏珊，Charlie生活中的妻子，Charlie的爸爸老戏骨Martin Sheen...众多名人美女穿梭其间。